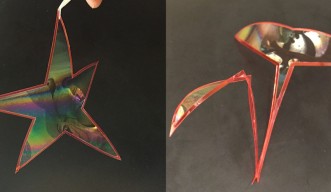Bursting the Bubble: Solution to the Kirchhoff-Plateau Problem

Often used for children’s enjoyment and artistic performances, soap bubbles are delicate, light-reflecting films that typically last just a few seconds before bursting. But beyond their value to entertain, soap bubbles are physical examples of the rich mathematical problem of minimal surfaces; they assume the shape of the least surface area possible, containing a given volume. Researchers at the Okinawa Institute of Science and Technology Graduate University (OIST) have recently worked out the solution to a mathematical problem — known as the Kirchhoff-Plateau problem — that is simply illustrated by soap films that span flexible loops.
“Our solution of the Kirchhoff–Plateau problem brings beautiful mathematical results close to what happens in the physical world,” says Dr. Giulio Giusteri, coauthor of the paper which was recently published in the Journal of Nonlinear Science. Dr. Giusteri worked with Professor Eliot Fried, who heads OIST’s Mathematical Soft Matter Unit, and Dr. Luca Lussardi from the Università Cattolica del Sacro Cuore in Italy.
The question answered by the team is a variant of the “Plateau problem”, a centuries-old mathematical problem, named after 19th century Belgian physicist, Joseph Plateau. Plateau hypothesized that when you dip a rigid wire frame into a soap solution, the surface of the soap film formed on the frame represents a minimum mathematically possible area, no matter the shape of the frame.
The first satisfactory solution for the Plateau problem was provided in the 20th century, by American mathematician Jesse Douglas, for which he was awarded the Fields Medal in 1936. More recently, in 2015, Professor Jenny Harrison from UC Berkeley and Harrison Pugh of Stony Brook University extended Douglas’s work, providing a proof valid under general hypotheses encompassing, for example, situations in which junctions are present where multiple soap films meet each other.

In contrast to the Plateau problem in which a soap film spans a fixed frame, the Kirchhoff-Plateau problem concerns the equilibrium shapes of soap films that span flexible loops, made, for instance, of fishing line, that can be described using Kirchhoff’s theory of rods — a model that provides a powerful approach for studying the statics and dynamics of thin elastic rods. The complication is that a flexible loop can change shape in response to the force exerted by the soap film. As such, a solution to the problem requires determining not only the shape of the soap film but also the shape of the bounding loop. In contrast, the shape of the boundary in the original Plateau problem is known because it is made of rigid wire that remains fixed against the relatively weak forces of the soap film.

An additional complication associated with the Kirchhoff-Plateau problem is that unlike the original Plateau problem in which the boundary is assumed to be one-dimensional, a Kirchhoff rod is a three-dimensional object. Although filaments like fishing line are thin, they are orders of magnitude thicker than a soap film in equilibrium, meaning that the area of the soap film can change depending on the point at which the film contacts the loop.
The researchers successfully translated all these physical effects into mathematical terms. As Prof. Fried explains: “No matter how strong the competition is between surface tension of the soap film and the elastic response of the loop, the system is always able to adjust to achieve a configuration of least energy.”
The solution to the Kirchhoff-Plateau problem not only contributes to the understanding of energy minimizing mathematical shapes, but can also be applied to biological systems. For instance, it could help us understand how the shape of a protein determines how it interacts with and binds to a surface.
The team is now working on computer simulations that, based on this mathematical model, can predict the behavior of physical systems.

Specialty
Research Unit
For press enquiries:
Press Inquiry Form